Statistical Hypotheses and Error

Hypotheses

• Null hypothesis (H₀₎
  • hypothesis of no difference
    • e.g., there is no link between disease and risk factor
• Alternative hypothesis (H₁₎
  • hypothesis of difference
•  e.g., there is a link between disease and risk factor

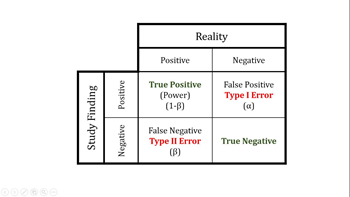
Type I Error (False Positive)

• Stating there is an association when none exits
  • incorrectly rejecting null hypothesis
• α = probability of type I error 
• p = probability that results as or more extreme than those of the study would be observed if the null hypothesis were true  
• general rule of thumb is that statistical significance is reached if p < 0.05

Type II Error (False Negative)

• Stating there is no effect when an effect exists 
  • incorrectly accepting null hypothesis 
• β = probability of type II error 

Power (True Positive)

• Probability of correctly rejecting null hypothesis 
  • power = 1 – β 
• Power depends on
  • sample size
    • increasing sample size increases power 
  • size of expected effect
• increasing effect size increases power

True Negative

• Probability of correctly accepting null hypothesis

Confidence Interval

• Range of values associated with a confidence level indicating the likelihood that the true population value of a parameter falls within that range
  • usually done with 95% confidence interval (2 standard deviations from the mean)
  • e.g., based on our study data, we are 95% confident that the average salary of a teacher lies between $30,000-45,000/year
• Confidence interval is calculated from statistics generated from the studied data
• Smaller confidence intervals suggest better precision of the data
• Larger confidence intervals suggest less precision of the data
• If confidence intervals of 2 groups overlap, there is no statistically significant difference

A Priori Versus Post Hoc Analysis

• A priori comparisons
  • comparisons planned prior to data analysis
  • planning dependent on knowledge researchers have prior to conducting statistical tests 
• Post hoc analysis
  • researcher decides additional comparisons to make after viewing data
  • choices dependent on knowledge researchers have gained after conducting statistical tests 
    • e.g., a test is run that says there is a difference between groups A, B, and C
      • post hoc analysis would involve comparing group A to group B, B to C, and A to C to see between which groups the difference lies 
    • one potential hazard is an increased likelihood of spurious statistical associations