Standard Deviation vs. Standard Error
- n = sample size
- Sigma (σ) = standard deviation
- SEM = standard error of the mean
- SEM = σ/√n
- SEM < σ
- SEM decreases as n increases
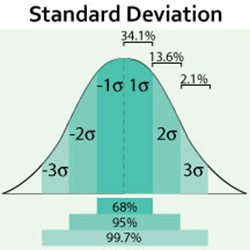
- z-scores
- 1 = +/- 1 σ around mean
- 2 = +/- 2 σ around mean
- 3 = +/- 3 σ around mean
Confidence Interval (CI)
- Describes the range in which the mean would be expected to fall if the study were performed again and again
- 95% CI (alpha = 0.05) is standard
- for 95% CI, Z = 1.96
- 95% CI (alpha = 0.05) is standard
- Outcomes
- if 0 falls within the CI when calculating the difference between 2 variables, H0 is not rejected and the result is not significant
- if 1 falls within the CI when calculating OR or RR, H0 is not rejected and the result is not significant
- Significance
- statistical significance refers to whether p < 0.05
- clinical significance requires that a statistically significant result be also clinically meaningful
T-test vs. ANOVA vs. χ2
- T-test
- compares the means of 2 groups on a continuous variable
- ANOVA (analysis of variance)
- χ2 (“chi-squared”)
- used with 2×2 tables
- e.g., effect of treatment on disease
Correlation Coefficient (r)
- Pearson coefficient, r, is always between -1 and +1
- Absolute value indicates strength of correlation between 2 variables
- Coefficient of determination = r2
Attributable Risk (AR)
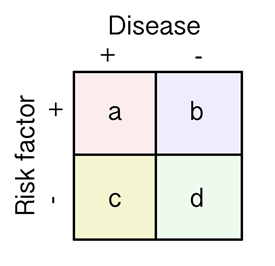
- AR is incidence in the exposed (Ie) – incidence in the unexposed (Iu) = Ie – Iu
- Ie = a/(a+b)
- Iu = c/(c+d)
- AR = a/(a+b) – c/(c+d)
- The AR percent (ARP) is the attributable risk divided by incidence in the exposed (Ie)
- ARP = 100* (Ie-Iu)/Ie = 100*[a/(a+b) – c/(c+d)]/[a/(a+b)]
- note that relative risk (RR) = Ie/Iu = a/(a+b) DIVIDED BY c/(c+d)
- using math tricks
- ARP = (RR-1)/RR